Формування акустичного поля у хвилеводі сферичним джерелом звуку
Основний зміст сторінки статті
Анотація
У даній роботі приведено постановку та часткове вирішення проблеми формування повного акустичного поля у хвилеводі з симетричними м’якими границями. Наведені вихідні та розрахункові співвідношення для прямого та відбитого поля акустичного тиску у хвилеводі з симетричними м’якими границями. Описані основні етапи отримання вказаних співвідношень, а також підхід та метод аналізу поля у хвилеводі для випадку, коли джерело звуку є не точковим, а сферичним.
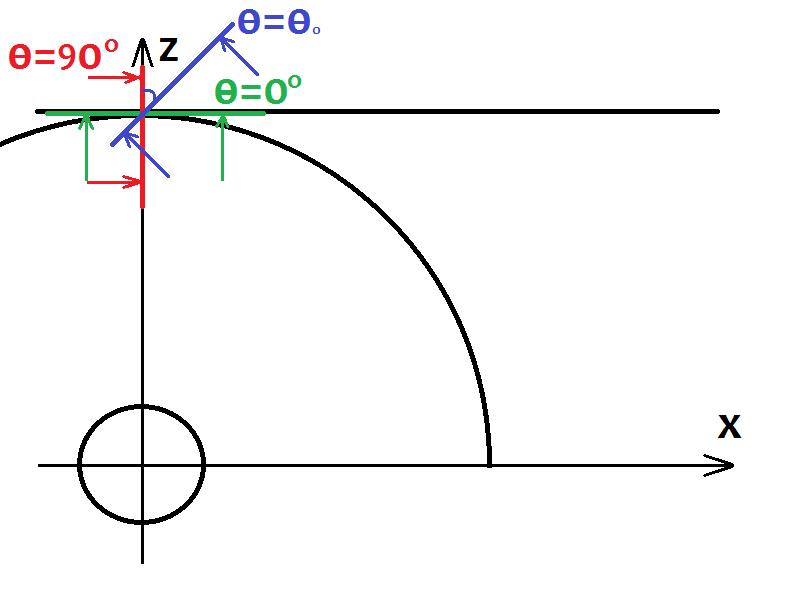
У роботі розглянуто симетричну задачу в межах першого квадранту.
Для аналізу відбитого поля пряме сферичне було представлене набором плоских нормальних хвиль. Співвідношення для відбитого поля були отримані завдяки розкладу сферичної хвилі на плоскі. Для опису апроксимованого відбитого поля уздовж вісі OZ було знайдено коефіцієнт відбиття. Отриманий коефіцієнт можна використовувати в подальших дослідженнях, зокрема, для розширення обчислень поля відбиття на весь перший квадрант, оскільки задача є симетричною. Це можна зробити за допомогою так званого методу уявного джерела.
Розрахунки в статті проводилися для різних глибин хвилеводу та робочих частот. У моделі хвилевод заповнено водою, а обмежено повітрям, тому границі хвилеводу акустично м'які.
Наведені у роботі співвідношення можуть бути використані в подальших дослідженнях. Оскільки задача є симетричною, то для розширення обчислень відбитого поля на всі чотири квадранти за допомогою так званого методу уявного джерела.
Для розрахунку відбитого поля у довільній точці першого квадранту приведені співвідношення, що залучають напрацювання щодо створених на межі хвилеводу зон Френеля.
Результати є базовими і можуть бути застосовані для формулювання та розв’язку задач озвучування мілких морів в рамках пружних та гідроелектропружних постановок.
Блок інформації про статтю

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Автори, які публікуються у цьому журналі, погоджуються з наступними умовами:- Автори залишають за собою право на авторство своєї роботи та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons Attribution License, котра дозволяє іншим особам вільно розповсюджувати опубліковану роботу з обов'язковим посиланням на авторів оригінальної роботи та першу публікацію роботи у цьому журналі.
- Автори мають право укладати самостійні додаткові угоди щодо неексклюзивного розповсюдження роботи у тому вигляді, в якому вона була опублікована цим журналом (наприклад, розміщувати роботу в електронному сховищі установи або публікувати у складі монографії), за умови збереження посилання на першу публікацію роботи у цьому журналі.
- Політика журналу дозволяє і заохочує розміщення авторами в мережі Інтернет (наприклад, у сховищах установ або на особистих веб-сайтах) рукопису роботи, як до подання цього рукопису до редакції, так і під час його редакційного опрацювання, оскільки це сприяє виникненню продуктивної наукової дискусії та позитивно позначається на оперативності та динаміці цитування опублікованої роботи (див. The Effect of Open Access).
Посилання
L.Brehovskih, Volnyi v sloistyih sredah [Waves in layered media], Moscow: Nauka, 1973.
K. Attenborough, «Review of ground effects on outdoor sound propagation from continuous broadband sources,» Applied Acoustics, № 24, pp. 229-319, 1988, DOI: 10.1016/0003-682X(88)90086-2.
G. Taraldsen, «A note on reflection of spherical waves,» № 117, pp. 3389-3392, June 2005, DOI: 10.1121/1.1904303.
R. Collin, «Hertzian dipole radiating over a lossy earth or sea: Some early and late 20th-century controversies,» IEEE Antennas and Propagation Magazine, № 46, pp. 64-79, 2004, DOI: 10.1109/MAP.2004.1305535.
T. F. W. Embleton, «Tutorial on sound propagation outdoors,» Journal of the Acoustical Society of America, т. 100, pp. 31-48, 1996, DOI: 10.1121/1.415879.
L. M. Brekhovskikh, Acoustics of Layered Media I–II, 2 ed., Berlin: Springer, 1999.
E. M. Salomons, Computational Atmospheric Acoustics, Dordrecht: Kluwer Academic Publishers, 2001.
A. Banos, Dipole radiation in the presence of a conducting half-space, Oxford: Pergamon Press, .
D. A. Bies, Engineering Noise Control, 2 ed., C. H. Hansen, Ed., CRC Press, 1996.
I. Rudnick, «Propagation of sound in the open air,» в Handbook of Noise Control, C. M. Harris, Edit., 1957.
F. P. Mechel, Formulas of Acoustics, Berlin: Springer, 2002.
I. Rudnick, «The propagation of an acoustic wave along a boundary,» Journal of the Acoustical Society of America, № 19, p. 348–356 , 1947, DOI: 10.1121/1.1916490.
U. Ingard, «On the reflection of a spherical sound wave from an infinite plane,» Journal of the Acoustical Society of America, № 23, p. 329–335, 1951, DOI: 10.1121/1.1906767.
C. F. Chien and W. W. Soroka, "Sound-propagation along an impedance," J. Sound Vib., no. 43, pp. 9-20, 1975, DOI: 0022-460X(75)90200-X.
C. F. Chien and W. W. Soroka, "A note on the calculation of soundpropagation along an impedance surface," J. Sound Vib., no. 69, pp. 340-343, 1980, DOI: 10.1016/0022-460X(80)90618-5.
B. Kassatkin, “Otrazhenie sfericheskoy volnyi na impedansnoy granitse razdela dvuh sred [Reflection of a spherical wave at the impedance interface of two media],”Scientific edition of Bauman MSTU. SCIENCE & EDUCATION. Bauman Moscow State Technical University. Issue: #12 2011, URL: http://technomag.edu.ru/doc/168640.html.
J. W. Li, T. Y. S., C. Dong and G. Tang, "A novel expression of the spherical-wave reflection coefficient at a plane interface," Geophysical Journal International, no. 211, pp. 700-717, 2017, DOI: 10.1093/gji/ggx308.
E. Shenderov, Volnovyiezadachigidroakustiki [Wave tasks of hydroacoustics], Leningrad, USSR: Sudostroenie, 1972.