Виявлення шумового сигналу в адитивній суміші на основі кумулянта другого порядку

Бічна панель сторінки статті

Залежність імовірності правильного виявлення
PDF
Опубліковано: чер 30, 2021
DOI: https://doi.org/10.20535/2617-0965.eae.227817
Ключові слова:
адитивна суміш, виявлення сигналу, дисперсія, закон розподілу, кумулянти, кумулянтний аналіз, точкова оцінка, шумова діагностика, шумова завада, шумовий сигнал

Основний зміст сторінки статті

Антон Єгорович Березницький
Національний технічний університет України «Київський політехнічний інститут імені Ігоря Сікорського»
https://orcid.org/0000-0001-8327-2519

Анотація

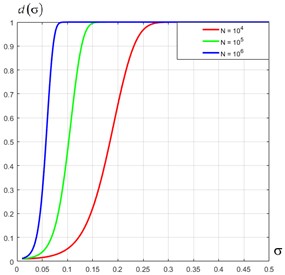
Проведено аналіз чутливості застосування кумулянта другого порядку адитивної суміші шумового сигналу і шумової завади до виявлення сигналу. Досліджувались нормальний, рівномірний та показниковий розподіли сигналу з різними середніми квадратичними відхиленнями, для завади – стандартний нормальний розподіл. Для ймовірності правильного виявлення сигналу 0,99 при ймовірності помилки першого роду 0,01 розраховано порогові значення та мінімальні об’єми вибірки, які забезпечують задані ймовірності, виходячи з гауссівського розподілу оцінки кумулянта другого порядку. Результати моделювання підтвердили розрахунки, експериментальна ймовірність правильного виявлення отримана не менше заданої.

Блок інформації про статтю

Як цитувати
Березницький, А. Є. (2021). Виявлення шумового сигналу в адитивній суміші на основі кумулянта другого порядку. Електронна та Акустична Інженерія, 4(2), 227817–1 . https://doi.org/10.20535/2617-0965.eae.227817
Номер
Том 4 № 2 (2021)
Розділ
Акустичні прилади та системи
Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Автори, які публікуються у цьому журналі, погоджуються з наступними умовами:

  1. Автори залишають за собою право на авторство своєї роботи та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons Attribution License, котра дозволяє іншим особам вільно розповсюджувати опубліковану роботу з обов'язковим посиланням на авторів оригінальної роботи та першу публікацію роботи у цьому журналі.
  2. Автори мають право укладати самостійні додаткові угоди щодо неексклюзивного розповсюдження роботи у тому вигляді, в якому вона була опублікована цим журналом (наприклад, розміщувати роботу в електронному сховищі установи або публікувати у складі монографії), за умови збереження посилання на першу публікацію роботи у цьому журналі.
  3. Політика журналу дозволяє і заохочує розміщення авторами в мережі Інтернет (наприклад, у сховищах установ або на особистих веб-сайтах) рукопису роботи, як до подання цього рукопису до редакції, так і під час його редакційного опрацювання, оскільки це сприяє виникненню продуктивної наукової дискусії та позитивно позначається на оперативності та динаміці цитування опублікованої роботи (див. The Effect of Open Access).

Посилання

A. I. Krasilnikov, V. S. Beregun, and T. A. Polobyuk, Kumuliantnye metody v zadachah shumovoi diagnostiki teploenergeticheskogo oborudovania [Cumulant methods in the problems of noise diagnostics of heat-power equipment]. Kyiv: Osvita Ukrainy, 2019, ISBN: 978-617-7777-98-3.

S. V. Babak, M. V. Myslovich, and R. M. Sysak, Statisticheskaya diagnostika electrotehnicheskogo oborudovaniya [Statistical diagnostics of electrical equipment]. Kyiv: Institut elektrodinamiki NAN Ukrainy, 2015, ISBN: 978-966-02-7704-5.

V. M. Baranov, A. I. Grizenko, and A. M. Karasevich, Acusticheskaya diagnostika i kontrol na predpriyatiah toplivno-energeticheskogo komplexa [Acoustic diagnostics and control at the enterprises of the fuel-energy complex]. Moskow: Nauka, 1998, ISBN: 5-02-003639-0.

V. S. Beregun, A. I. Krasilnikov, and T. A. Polobyuk, “ANALYSIS OF THE INFLUENCE OF FILTRATION ON THE SENSITIVITY OF THE CUMULANT METHOD OF DETECTING THE ACOUSTIC SIGNALS OF LEAKAGE,” Ind. Heat Eng., vol. 40, no. 2, pp. 78–83, Jun. 2018, DOI: https://doi.org/10.31472/ihe.2.2018.11.

V. S. Beregun and A. I. Krasilnikov, “RESEARCH OF EXCESS KURTOSIS SENSITIVENESS OF DIAGNOSTIC SIGNALS FOR CONTROL OF THE CONDITION OF THE ELECTROTECHNICAL EQUIPMENT,” Tekhnichna Elektrodynamika, vol. 2017, no. 4, pp. 79–85, Jun. 2017, DOI: https://doi.org/10.15407/techned2017.04.079.

V. Beregun and A. Krasilnikov, “The Use of Cumulant Methods for Distinction of Diagnostic Signals with Gamma Distribution,” in 2020 IEEE 40th International Conference on Electronics and Nanotechnology (ELNANO), 2020, pp. 741–746, DOI: https://doi.org/10.1109/ELNANO50318.2020.9088804.

S. I. Builo, “Physico-Mechanical, Chemical and Statistical Aspects of Acoustic Emission,” Izv. Altai State Univ., no. 1, 2019, DOI: https://doi.org/10.14258/izvasu(2019)1-01.

A. N. Malahov, Kumuliantny analis sluchaynyh negaussovyh prozessov i ih preobrazovaniy [Cumulant analysis of random non-Gaussian processes and their transformations]. Moskow: Sovetskoe radio, 1978.

E. Palahina, M. Gamcová, I. Gladišová, J. Gamec, and V. Palahin, “Signal Detection in Correlated Non-Gaussian Noise Using Higher-Order Statistics,” Circuits, Syst. Signal Process., vol. 37, no. 4, pp. 1704–1723, Apr. 2018, DOI: https://doi.org/10.1007/s00034-017-0623-5.

V. S. Beregun, O. V. Harmash, and A. I. Krasil’nikov, “Srednekvadratichiskie oshybki ozenok kumulantnyh koefizientov piatogo i shestogo poriadkov [RMS errors of estimates of cumulant coefficients of the fifth and sixth orders],” in Electronnoe modelirovanie, 2014, pp. 17–28.

V. V. Palagin, O. V. Ivchenko, and D. A. Wedernikov, Statystychne ozinuvannya parametriw negaussovyh korelovanyh wypadkovyh prozesiw [Statistical estimation of parameters of non-Gaussian correlated random processes]. Cherkasy: Cherkasky derjavny tehnologichny universytet, 2018, ISBN: 978-966-9730-36-7.

V. Beregun and O. Harmash, “Application of Cumulant Coefficients for Solving the Problems of Testing and Diagnostics in Control Systems,” in 2018 IEEE 5th International Conference on Methods and Systems of Navigation and Motion Control (MSNMC), 2018, pp. 210–213, DOI: https://doi.org/10.1109/MSNMC.2018.8576176.

A. Krasilnikov, V. Beregun, and O. Harmash, “Analysis of Estimation Errors of the Fifth and Sixth Order Cumulants,” in 2019 IEEE 39th International Conference on Electronics and Nanotechnology (ELNANO), 2019, pp. 754–759, DOI: https://doi.org/10.1109/ELNANO.2019.8783910.

A. I. Krasil’nikov and V. S. Beregun, “Analysis of Estimation Error of Skewness and Kurtosis of Bunimovich-Rice Processes with Exponentially Power Waveform of Pulses,” Radioelectron. Commun. Syst., vol. 63, no. 8, pp. 430–440, Aug. 2020, DOI: https://doi.org/10.3103/S0735272720080051.

S. W. Zabolotnii, S. S. Martynenko, and S. V. Salypa, “Method of Verification of Hypothesis about Mean Value on a Basis of Expansion in a Space with Generating Element,” Radioelectron. Commun. Syst., vol. 61, no. 5, pp. 222–229, May 2018, DOI: https://doi.org/10.3103/S0735272718050060.

Z. L. Warsza and S. V. Zabolotnii, “Polynomial estimation of the measurand parameters for samples from non-Gaussian distributions based on higher order statistics,” 2018, pp. 383–400, URL: https://www.worldscientific.com/doi/abs/10.1142/9789813274303_0039.

H. Cramér, Mathematical Methods of Statistics. Princeton University Press, 1999, ISBN: 978-1-4008-8386-8.

A. Stuart and K. Ord, Kendall’s Advanced Theory of Statistics, Vol. 1. Distribution Theory. Wiley, 2010, ISBN: 978-0470665305.

B. U. Lemeshko, S. B. Lemeshko, S. N. Postowalov, and E. W. Chimitova, Statisticheskiy analis dannyh, modelirowanie i issledowanie veroyatnosnyh zakonomernostey. Komputerny podhod [Statistical analysis of data, modeling and investigation of probable patterns. Computer approach]. Novosibirsk: NGTU, 2011, ISBN: 978-5-7782-1590-0.

V. P. Diakonov, MATLAB i SIMULINK dlia radioinjenerov [MATLAB and SIMULINK for radio engineers]. Moskow: DMK Press, 2011.

R. N. Vadzinskiy, Spravochnic po veroyatnosnym raspredeleniam [Handbook on probability distributions]. SPb: Nauka, 2001, ISBN: 5-02-024919-X.