Алгебраїчна характеристика класу матричних перетворень та її апаратна реалізація

Анотація

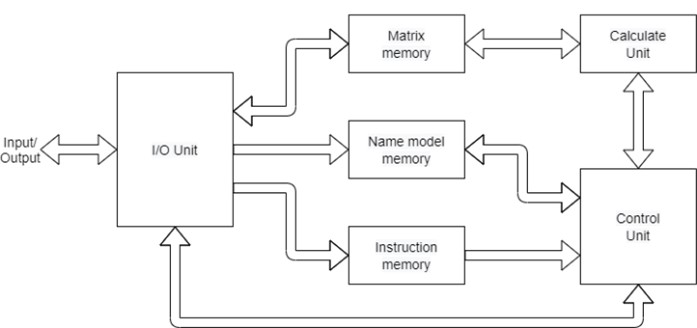
У даній роботі на основі примітивних програмних алгебр виводиться алгебраїчна характеристика класу матричних перетворень методом ізоморфних відображень на алгебраїчну характеристику классу векторних перетворень. В роботі також описано апаратну реалізацію прискорювача матричних операцій на основі отриманих даних. Актуальність роботи обумовлена тим, що сьогодні відбувається стрімке проникнення  комп'ютерних технологій в усі сфери життєдіяльності соціуму і, як наслідок, кількість даних, які потрібно опрацювати за одиницю часу постійно зростає. Велика кількість задач, пов’язаних зі значними об’ємами складних обчислень вирішується методами, що ґрунтуються на матричних операціях. Тож дослідження матричних обчислень та їх прискорення є досить важливою задачею. У даній роботі в якості внеску в даному напрямку пропонується  дослідження класу матричних перетворень за допомогою сигнатурних операцій примітивної програмної алгебри – багатомісної суперпозиції, галуження й циклування, що представляють собою уточнення найбільш поширених управлінських структур у більшості високорівневих мов програмування, а також ізоморфного відображення. Сигнатурні операції примітивної програмної алгебри в поєднанні з базовими частково-рекурсивними матричними функціями та предикатами дозволяють реалізувати множину усіх частково-рекурсивних матричних функцій та предикатів. Отримано результат про базис матричної примітивної програмної алгебри. Ізоморфізм забезпечує відтворення частково-рекурсивних функцій та предикатів для матричних перетворень як образів частково-рекурсивних векторних функцій та предикатів. Повноту алгебраїчної системи матричних перетворень забезпечено завдяки наявним результатам по виведенню повноти алгебраїчної системи для векторних перетворень. Створена іменна модель матричних даних, оптимізована під використання в розробці апаратної реалізації. В апаратній реалізації забезпечена підтримка сигнатурних операцій примітивної програмної алгебри та реалізована апаратна підтримка ізоморфного відображення. Реалізована апаратна підтримка функцій суми, множення та транспонування матриць, а також предиката рівності двох матриць. Підтримка сигнатурних операцій примітивної програмної алгебри забезпечується проектуванням контролюючої частини матричного обчислювального апарату на основі архітектури RISC. В основі апаратної підтримки ізоморфізму лежать лічильники, вони дозволяють інтуїтивно реалізувати циклування у функціях ізоморфних відображень. Швидке виконання векторних операцій забезпечується принципом комп’ютерних обчислень SIMD.